Quantum Markov chain

In mathematics, the quantum Markov chain is a reformulation of the ideas of a classical Markov chain, replacing the classical definitions of probability with quantum probability. Very roughly, the theory of a quantum Markov chain resembles that of a measure-many automata, with some important substitutions: the initial state is to be replaced by a density matrix, and the projection operators are to be replaced by positive operator valued measures.

More precisely, a quantum Markov chain is a pair $(E,\rho)$ with $\rho$ a density matrix and $E$ a quantum channel such that

$E:\mathcal{B}\otimes\mathcal{B}\to\mathcal{B}$

is a completely positive trace-preserving map, and 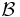$\mathcal{B}$ a C^*-algebra of bounded operators. The pair must obey the quantum Markov condition, that

$\operatorname{Tr} \rho (b_1\otimes b_2) = \operatorname{Tr} \rho E(b_1, b_2)$

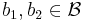for all $b_1,b_2\in \mathcal{B}$ .